
GPU Milkdrops
This offline GPU implementation of a Vorton Method was written in late 2013 out of personal interest. It was later extended to do real-time simulation, with some tradeoffs in quality.
Conceptually, vorton methods are simple. The idea is to discretize the velocity-vorticity form of the Navier-Stokes equation with vorton particles, each carrying some vorticity. That is, many particles are placed in the fluid, each inducing a tiny vortex around themselves, spinning around some axis. The velocity of the fluid can then be evaluated at any point in space as the sum of the velocities induced by each vortex, which is also described by Biot-Savart Law. Advecting the particles is then as simple as integrating through the induced velocity field.
As long as no boundaries are involved, this is very simple to implement. Unfortunately, it is also slow - the naive approach has quadratic runtime in the number of particles. To achieve high numbers of particles (and therefore high detail), an approximate approach described in A hierarchical O(N log N) force-calculation algorithm by Barnes and Hut comes in handy.
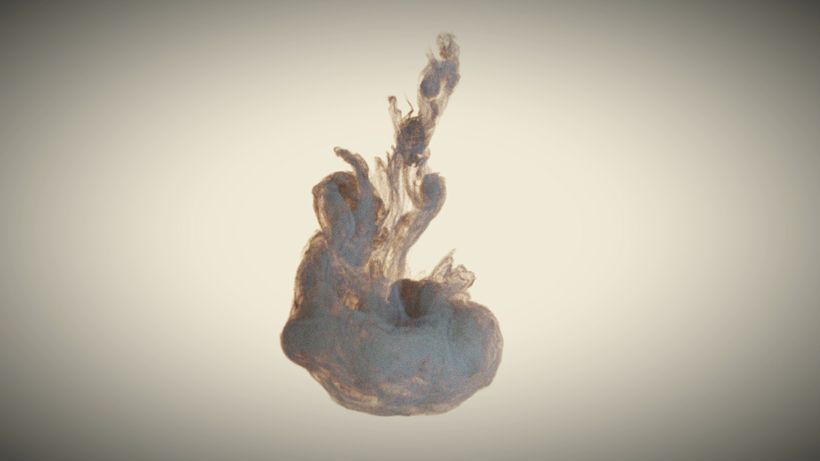
A milky, black drop of ink descends into water
The basic idea of the Barnes-Hut algorithm is that particles which are close to an evaluation point are much more important than those which are far away. Therefore, particles far away can be approximated without too much impact on the quality of the solution. In particular, groups of particles which are far away and close to each other can be clustered and replaced with a single "super particle" that has higher contribution, but is cheaper to evaluate.
To achieve this, the original Barnes-Hut algorithm uses an octree data structure, which works well, but is difficult to implement efficiently on GPUs. For this project, I instead used hierarchical grids, which integrate extremely well with existing GPU hardware facilities such as texturing units and rasterization. Ultimately the implementation ended up just being tedious and did not require any clever GPU tricks.
For rendering, I also implemented a volumetric GPU path tracer that can render arbitrary homogeneous participating media with spatially varying density. No clever importance sampling techniques were used, and as a result, noise-free videos could take several days or weeks to render.
Finally, with some simplifications and quality reductions, I was able to achieve real-time simulation at 60FPS on the GPU, shown in the video below. Rendering is also performed at 60FPS using multiple passes and rudimentary volumetric shading and emission using shadow volumes. Since it does not support solid obstacles, mushroom clouds are about the most exciting thing the program can simulate, but for a real-time effect it holds up quite nicely.
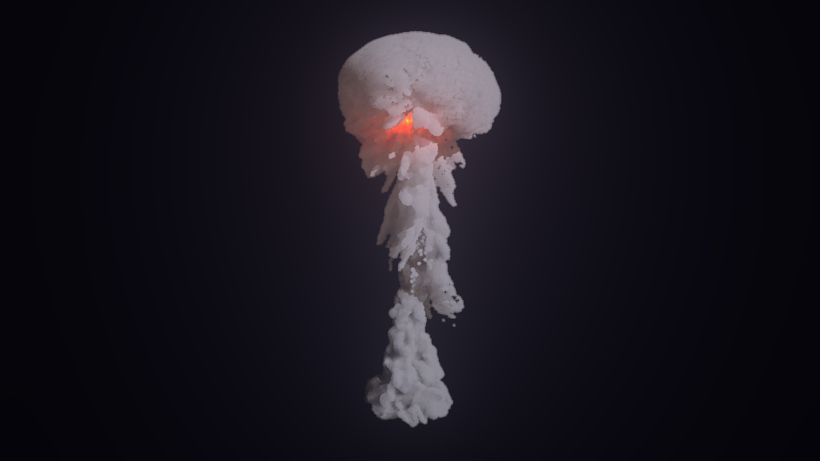
A realtime (60FPS) GPU simulation of a mushroom cloud ascending